Utilising the GPU for rigid body physics calculations – Part 3 – Full Primitive Collisions Detection
If you missed Part 1 or Part 2 in the series on GPU Rigid Body Physics – Check them out First!

Goal:
To allow the use of a selection of rigid body colliders for units in the game
Technique:
Implementing SAT for a range of primitives
Reasoning:
SAT provides efficient collision detection
It’s now 2025, and while re-working the in game physics logic it was decided that now was an appropriate time to improve the collision detection of units. While our raycasts work fine for uneven box shaped units, this doesn’t work for collisions between the units. And as we will shortly be adding in non-uniform unit types (long drones?), a more fundamental improvement initiative was started!
Given the expected shapes of objects it was decided that box and ellipsoid colliders would be needed, with the future intention that any more complex larger units would use compound collision detection, with all compound elements being made up of boxes or ellipsoids. Given we already have the concept of parents and children for units on the GPU side this should be pretty easy to implement when required.
For now two main types of collisions are required:
- Does a ray from a certain point and direction collide with a unit
- Given a certain direction, how far away is the bounding box of the unit from its centre point
This could re-use the same bounding box algorithms – OOB and Ellipsoid, in addition, sphere and AABB would be included for instances where there is no rotation for efficiency purposes. This should provide a comprehensive base to build up from
Next stop – actual collision detection. As we can can no longer use distances from centre points (where all objects are spheres) things get a bit more complicated. Its still going to be worth having point colliders, as well as box and ellipsoid. I’m sure it would be possible to do some clever maths where a single function / approach handles all the different interactions of these, but for development and my own sanity when testing we’re going to develop and test each combination of objects separately.
We’ve looked at different methodologies. Mainly the same SAT (Separated Axis Theorem) approach used in the Raycast work in part 2 of this series, and also something called GJK. GJK can be more efficient for some shapes, but requires more work to produce normals, so we are still using the SAT methodology in most cases for non-point objects. To recap – this essentially relies on checking for any separating of objects between all relevant axis. If no axis has a gap then we know the objects must be overlapping!
Setup
First, let’s setup our collision result. What do we need to know when a collision occurs to process it effectively? We need to know if it happened, we need to know how far overlapping the objects are, and we need to know and angle of the collision. Here is a simple struct we can use to store this information along with a simple initialiser to set default values
//Data Returned From A Collision
struct CollisionResult {
bool collided;
float depth;
float3 normal;
};
//Simple HLSL initialiser
void DefaultCollision(CollisionResult result) {
result.collided = false;
result.depth = 0.0;
result.normal = float3(0, 0, 0);
}You might notice that we are missing the actual collision point. The reason for this is twofold:
- 1) We don’t really need it. We can calculate required position and velocity adjustments for a good simulation without it. Knowing the actual collision point is mainly important if we want to do things like apply torque/rotational velocity to our objects based on the collisions, or have objects resting on each other, but while this would be nice its not vital for our game right now
- 2) It requires quite a lot of additional calculations for non-point collisions
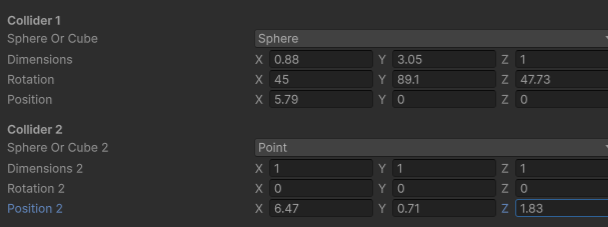
We’ve done a bit of setup so that input parameters for each object can be controlled from the editor as shown below.
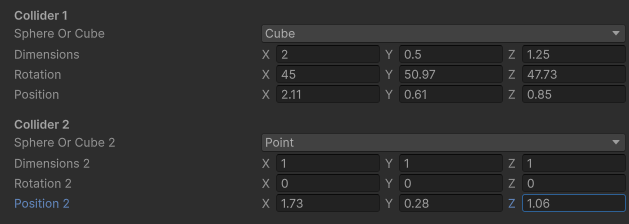
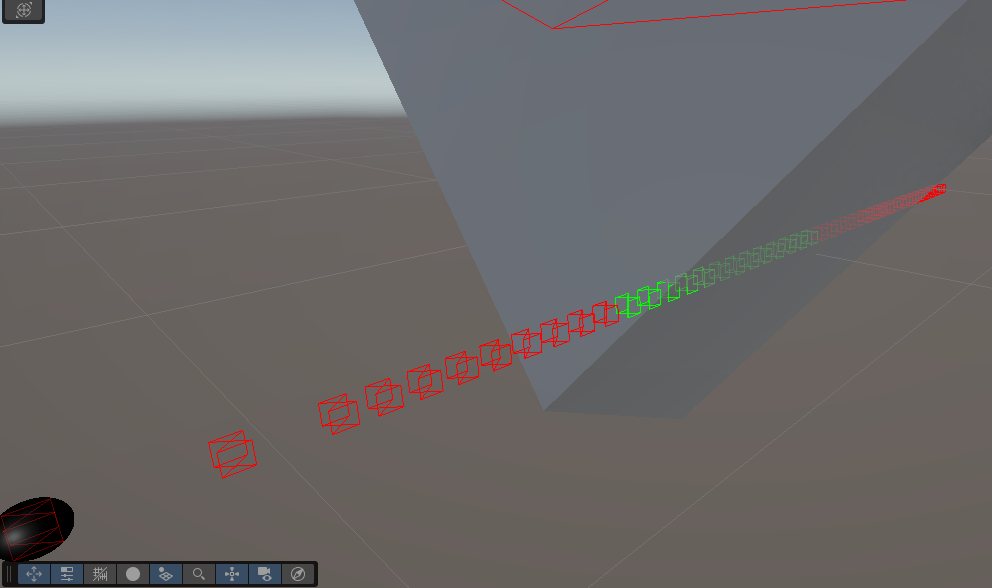
Then added in an on screen visualiser so we can immediately see where collisions are found and understand what’s going on. As we move the objects around the collision detection is regularly refreshed and and coloured outline is produced to illustrate where the test occurred, and if there was a hit. Green shows there was a collision and Red that there is no collision.
So, for all the different variations we’ve setup a nice simple selector function in the compute shader. Initially we cast the broad shape types we have before into the more generic types we are going to use for collision detection (AABB & OBB into Box type, Sphere and Ellipsoid into Ellipsoid type).
Then we simply check which two types we are comparing, and run the relevant function. It’s worth noting the order does matter (i.e. point and box needs slightly different processing than box and point) – as for instance in the pointBoxCollide function, we only take the position of the point, but also take rotation and size of the box.
bool CalculateCollisions(
float3 center, float3 dimensions, float3 rotation, int shapeTypeI /* 0 = AABB, 1 = OBB , 2 = Sphere, 3 = Ellipsoid */,
float3 center2, float3 dimensions2, float3 rotation2, int shapeType2I /* 0 = AABB, 1 = OBB , 2 = Sphere, 3 = Ellipsoid */)
{
int simpleShapeType = -1; // -1 Point, 0 Box, 1 Ellipsoid
int simpleShapeType2 = -1; // -1 Point, 0 Box, 1 Ellipsoid
if (shapeTypeI == 1 || shapeTypeI == 0) {
simpleShapeType = 0;
}
if (shapeTypeI == 2 || shapeTypeI == 3) {
simpleShapeType = 1;
}
if (shapeType2I == 1 || shapeType2I == 0) {
simpleShapeType2 = 0;
}
if (shapeType2I == 2 || shapeType2I == 3) {
simpleShapeType2 = 1;
}
float4x4 rot = CreateRotationMatrix4x4(rotation, true);
float4x4 rot2 = CreateRotationMatrix4x4(rotation2, false);
bool hit = false;
if (simpleShapeType == -1 && simpleShapeType2 == -1) {
hit = pointPointCollide(center, center2, true);
} else if (simpleShapeType == -1 && simpleShapeType2 == 0) {
hit = pointBoxCollide(center, center2, rot2, dimensions2, true);
} else if (simpleShapeType == 0 && simpleShapeType2 == -1) {
hit = pointBoxCollide(center2, center, rot, dimensions, false);
} else if (simpleShapeType == -1 && simpleShapeType2 == 1) {
hit = pointEllipsoidCollide(center, center2, rot2, dimensions2, true);
} else if (simpleShapeType == 1 && simpleShapeType2 == -1) {
hit = pointEllipsoidCollide(center2, center, rot, dimensions, false);
} else if (simpleShapeType == 0 && simpleShapeType2 == 0) {
hit = boxBoxCollide(center, rot, dimensions, center2, rot2, dimensions2, true);
} else if (simpleShapeType == 0 && simpleShapeType2 == 1) {
hit = boxEllipsoidCollide(center, rot, dimensions, center2, rot2, dimensions2, true);
} else if (simpleShapeType == 1 && simpleShapeType2 == 0) {
hit = boxEllipsoidCollide(center2, rot2, dimensions2, center, rot, dimensions, true);
} else if (simpleShapeType == 1 && simpleShapeType2 == 1) {
hit = ellipsoidEllipsoidCollide(center, rot, dimensions, center2, rot2, dimensions2, true);
}
return hit;
}As you can see above, we have 6 discrete combinations of collider types which will each be handled slightly differently. We also have a parameter at the end of each function which define whether the primary object (i.e. object 1) is supplied first in the parameter list. This ensure we can return a collision normal that is always relative to the primary object
Point vs. Point Collision Detection
The simplest check is Point vs. Point – I can’t actually think of many situations where this is likely to be useful, but we’ve added it in for completeness. All we need for point collisions is a simple distance check, with a small enough tolerance. Easy! This is quite a unique case as a point has no volume, we’ve derived a simple collision normal based on the relative velocities of the two point objects.
// --- Point vs. Point ---
CollisionResult pointPointCollide(float3 point1Pos, float3 point2Pos, float3 point1Vel, float3 point2Vel, bool primaryFirst) {
CollisionResult result;
DefaultCollision(result); //Set default values
float distSq = lengthSquared(point1Pos - point2Pos);
float tolerance = 0.0001; // Use a tolerance!
if (distSq < tolerance) {
result.collided = true;
result.depth = sqrt(tolerance) - sqrt(distSq); // Calculate penetration depth
// Calculate relative velocity
float3 relativeVelocity = primaryFirst ? point1Vel - point2Vel : point2Vel - point1Vel;
// Normalize the relative velocity to get the collision normal
if (lengthSquared(relativeVelocity) > 0.0001) {// Avoid division by zero
result.normal = normalize(relativeVelocity);
}
}
return result;
}Point vs. Box Collision Detection
One down, five to go! Let’s hope they’re all as easy. Next up Point vs. Box collision. The logic for this isn’t too difficult, as the point only has a position we can easily apply the inverse of any box rotation to the point, to get it into the axis aligned space of the box.
Then in each of the boxes three aligned axis we either take the local point if its inside the box extends, or take the extents (box faces) if the local point is outside. In this way if localPoint is inside the box, closestPoint will be equal to localPoint. If localPoint is outside the box, closestPoint will be on one of the faces, edges, or corners of the box. We can then take the distance between these, with a value of 0 implying that the local point is inside the box.
Given a collision occurs, we then proceed to calculate the collision depth and normal. We simply find which axis edge is closest (X, Y or Z), and then get the surface normal of the box in that direction.
// --- Point vs. Box ---
CollisionResult pointBoxCollide(float3 pointPos, float3 boxPos, float4x4 boxRotation, float3 boxExtents, bool primaryFirst) {
CollisionResult result;
DefaultCollision(result); //Set default values
// Transform the point into the box's local space
float3 localPoint = mul(transpose(boxRotation), float4(pointPos - boxPos, 0)).xyz;
// Find closest point on box to localPoint
float3 closestPoint = clamp(localPoint, -boxExtents, boxExtents);
// Calculate distance squared between localPoint and closestPoint
float distSq = lengthSquared(localPoint - closestPoint);
if (distSq < 0.0001) { // Use a small tolerance
result.collided = true;
// Calculate penetration depth and normals
float3 delta = abs(localPoint) - boxExtents;
float3 absDelta = abs(delta);
if (absDelta.x < absDelta.y && absDelta.x < absDelta.z) {
result.depth = -delta.x;
result.normal = mul(boxRotation, float4(sign(localPoint.x), 0, 0, 0)).xyz; // Normal along X-axis
} else if (absDelta.y < absDelta.z) {
result.depth = -delta.y;
result.normal = mul(boxRotation, float4(0, sign(localPoint.y), 0, 0)).xyz; // Normal along Y-axis
} else {
result.depth = -delta.z;
result.normal = mul(boxRotation, float4(0, 0, sign(localPoint.z), 0)).xyz; // Normal along Z-axis
}
result.normal = normalize(result.normal);
if (primaryFirst) { //Invert normal if required
result.normal = -result.normal;
}
}
return result;
}As a side note – It’s important to be very careful with this kind of math is when inverting a matrix. There are two functions that can be used – transpose and invert. Transpose simple flips all the matrix elements along the diagonal central line. Invert however explicitly creates the mathematical inverse (such that M * MI = Identity Matrix). In the case of rotations however, the transpose matrix is the same as the inverse matrix! You might wonder why not just calculate the inverse since that is always correct. Well, the main reason is performance, calculating a transpose is easy and quick with no actual calculations, you just move elements around. Invert however requires lots of heavy maths, so we avoid it where possible.
Point vs. Ellipsoid Collision Detection
Right then, these point collisions seem pretty straight forward, just one more to go (and then it’s on to the hard stuff!). And what do you know – it turns out the same approach as for the box works here, we reverse any ellipsoid rotation from the point. Then by dividing the point position be the extents we are treating the ellipsoid as a 1 unit sized sphere. Finally we check if the distance from the centre of the sphere is <1, to determine if the point sits within the sphere to get our collided value.
Then the depth and normal can be calculated in a similar way to with the box collider.
// --- Point vs. Ellipsoid ---
CollisionResult pointEllipsoidCollide(float3 pointPos,
float3 ellipsoidPos, float4x4 ellipsoidRotation, float3 ellipsoidExtents, bool primaryFirst)
{
CollisionResult result;
DefaultCollision(result); //Set default values
// Transform the point into the ellipsoid's local space
float3 localPoint = mul(transpose(ellipsoidRotation), float4(pointPos - ellipsoidPos, 0)).xyz;
// Scale the point by the ellipsoid's extents
float3 scaledPoint = localPoint / ellipsoidExtents;
float distSq = lengthSquared(scaledPoint);
if (distSq <= 1.0) {
result.collided = true;
float dist = sqrt(distSq);
result.depth = 1.0 - dist; // Penetration depth
// Calculate normal in local space, then transform to world space
result.normal = mul(ellipsoidRotation, float4(normalize(scaledPoint), 0)).xyz;
result.normal = normalize(result.normal);
if (primaryFirst) { //Invert normal if required
result.normal = -result.normal;
}
}
return result;
}It’s probably worth just illustrating again how we are testing these functions. Essentially adding on sufficient transformation of position, rotation and scale to the ellipsoid, and then moving the point particle around and checking the collisions occur where we expect them to. Remember, there is no point rotating or scaling as the point object as it has not volume! The black lines you can see are an illustration of the collision normals (although note the are not projected out from the collision point as this is not calculated, instead they are just projected from the centre of the object)
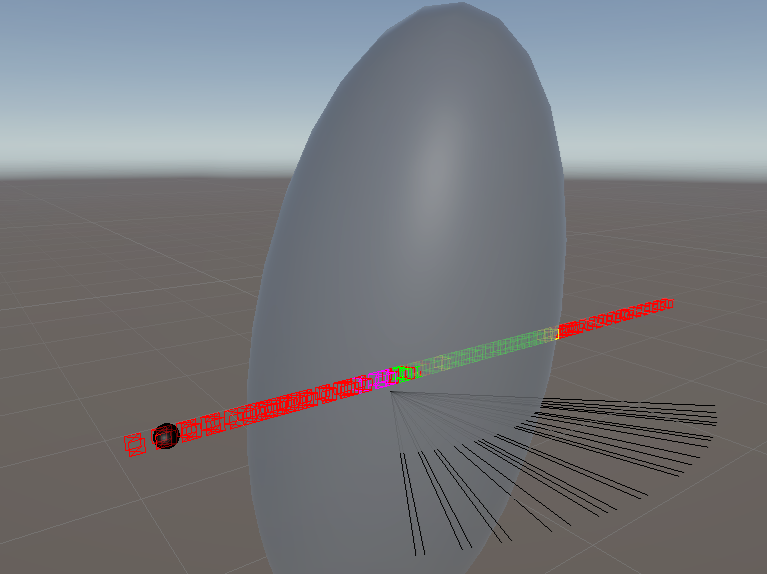
Box vs Box Collision Detection
Ok, this is where things start to get a little more complicated, we can’t take any shortcuts, both our objects are actual 3D volumes with any potential rotation and scaling factors applied. Unlike before where one object was a point, we can’t just rotate into the other objects axis aligned space without move out of our own starting one.
Given there is not single ‘aligned axis’ space we can use to simplify our calculations the approach we are going to use is to look at all of the individual axis. The maths behind it gets quite complicated, but essentially if we apply Separated Axis Theorem to:
- All the axis of box1 (3 axis)
- All the axis of box2 (3 axis)
- All the axis perpendicular, to each combination of the above (9 axis [3×3])
If there are no separating axis across any of these, then we know that the boxes overlap! We still have the problem of representing our boxes in each of these axis. For that we have a projection function which will produce the minimum and maximum extents of the input box along the axis specified.
// Rotated extents, often referred to as half-extents or radius
struct float3_rotated {
float3 x;
float3 y;
float3 z;
};
void projectBox(float3 axis, float3 center, float3_rotated extents, out float minProj, out float maxProj){
float centerProj = dot(axis, center);
float extentProj = abs(dot(axis, extents.x)) + abs(dot(axis, extents.y)) + abs(dot(axis, extents.z));
minProj = centerProj - extentProj;
maxProj = centerProj + extentProj;
}Ok, so given all that, here is the function. You can see we setup the 15 axis to be checked. Then check each of them in turn for separation. If no separation is found then we have a collision! We also take the collision normal & depth from the smallest overlapping axis. We take the smallest overlap as this represents the smallest distance we need to add to separate the objects.
// --- Box vs. Box (SAT) ---
CollisionResult boxBoxCollide(float3 box1Pos, float4x4 box1Rotation, float3 box1Extents,
float3 box2Pos, float4x4 box2Rotation, float3 box2Extents, bool primaryFirst)
{
CollisionResult result;
result = DefaultCollision(result); //Set default values
float3_rotated box1ExtentsRotated;
box1ExtentsRotated.x = mul(box1Rotation, float3(box1Extents.x, 0, 0));
box1ExtentsRotated.y = mul(box1Rotation, float3(0, box1Extents.y, 0));
box1ExtentsRotated.z = mul(box1Rotation, float3(0, 0, box1Extents.z));
float3_rotated box2ExtentsRotated;
box2ExtentsRotated.x = mul(box2Rotation, float3(box2Extents.x, 0, 0));
box2ExtentsRotated.y = mul(box2Rotation, float3(0, box2Extents.y, 0));
box2ExtentsRotated.z = mul(box2Rotation, float3(0, 0, box2Extents.z));
// 15 axes to test: 3 box1 axes, 3 box2 axes, 9 cross products.
float3 axes[15] =
{
box1ExtentsRotated.x, box1ExtentsRotated.y, box1ExtentsRotated.z, // Box 1 axes
box2ExtentsRotated.x, box2ExtentsRotated.y, box2ExtentsRotated.z, // Box 2 axes
cross(box1ExtentsRotated.x, box2ExtentsRotated.x), cross(box1ExtentsRotated.x, box2ExtentsRotated.y), cross(box1ExtentsRotated.x, box2ExtentsRotated.z),
cross(box1ExtentsRotated.y, box2ExtentsRotated.x), cross(box1ExtentsRotated.y, box2ExtentsRotated.y), cross(box1ExtentsRotated.y, box2ExtentsRotated.z),
cross(box1ExtentsRotated.z, box2ExtentsRotated.x), cross(box1ExtentsRotated.z, box2ExtentsRotated.y), cross(box1ExtentsRotated.z, box2ExtentsRotated.z)
};
float minOverlap = 1e20; // Initialize with a large value.
for (int i = 0; i < 15; i++) {
if (lengthSquared(axes[i]) < 0.0001) // Skip near-zero axes (from cross products)
continue;
float3 axis = normalize(axes[i]);
float box1Min, box1Max, box2Min, box2Max;
projectBox(axis, box1Pos, box1ExtentsRotated, box1Min, box1Max);
projectBox(axis, box2Pos, box2ExtentsRotated, box2Min, box2Max);
// Check for separation along this axis
if (box1Max < box2Min || box2Max < box1Min) {
result.collided = false;
return result; // Separating axis found!
}
// Calculate overlap along the current axis
float overlap = min(box1Max, box2Max) - max(box1Min, box2Min);
if (overlap < minOverlap) {
minOverlap = overlap;
// Ensure normal points from box1 towards box2
result.normal = dot(box2Pos - box1Pos, axis) > 0 ? axis : -axis;
result.depth = overlap;
}
}
result.normal = normalize(result.normal);
if (primaryFirst) { //Invert normal if required
result.normal = -result.normal;
}
result.collided = true;
return result; // No separating axis found. Must be colliding
}As a little extra efficiency we have added in a bounding sphere check to our boxBoxCollider function – this allows for a much quicker rejection test before deciding to complete the full SAT test which requires substantially more calculations.
// --- Bounding Sphere Check ---
float box1Radius = sqrt(dot(box1Extents, box1Extents));
float box2Radius = sqrt(dot(box2Extents, box2Extents));
float combinedRadius = box1Radius + box2Radius;
float distSq = lengthSquared(box2Pos - box1Pos);
if (distSq > combinedRadius * combinedRadius) {
// Bounding spheres don't intersect. Boxes definitely don't collide.
return result; // Early out - no collision.
}Ellipsoid vs Ellipsoid Collision Detection
Ok, now we’re making good progress. But things have suddenly got a bit more difficult. SAT is very well suited to polyhedra, with a discrete number of sides (and therefore axis to check), however ellipses have infinite sides and therefore would require infinite edge checks to get perfectly right. So SAT is not necessarily the best approach for this, but let’s see how well it goes. We initially tried to reduce the number of axis down to 6, but this led to significant errors, so went back up to 15 as with the other functions. This appears to be reasonable.
// Project an ellipsoid onto an axis.
void projectEllipsoid(float3 axis, float3 center, float4x4 rotation, float3 extents, out float minProj, out float maxProj)
{
// Transform the axis into the ellipsoid's local space.
float3 invRotAxis = mul(transpose(rotation), float4(axis, 0)).xyz; //inverse rotation, expensive!
invRotAxis = normalize(invRotAxis);
// Calculate the projection radius. Key optimization: avoid sqrt() in length()
float radius = sqrt(lengthSquared(invRotAxis * extents));
float centerProj = dot(center, axis);
minProj = centerProj - radius;
maxProj = centerProj + radius;
}// --- Ellipsoid vs. Ellipsoid (Simplified SAT/Bounding Sphere Check) ---
CollisionResult ellipsoidEllipsoidCollide(float3 ellipsoid1Pos, float4x4 ellipsoid1Rotation, float3 ellipsoid1Extents,
float3 ellipsoid2Pos, float4x4 ellipsoid2Rotation, float3 ellipsoid2Extents, bool primaryFirst)
{
CollisionResult result;
result = DefaultCollision(result); //Set default values
// Fast bounding sphere check.
float combinedRadius = max(ellipsoid1Extents.x, max(ellipsoid1Extents.y, ellipsoid1Extents.z)) +
max(ellipsoid2Extents.x, max(ellipsoid2Extents.y, ellipsoid2Extents.z));
if (lengthSquared(ellipsoid2Pos - ellipsoid1Pos) > combinedRadius * combinedRadius)
{
result.collided = false;
return result; // Bounding spheres don't overlap.
}
// Test the ellipsoid's axes.
float3 ellipsoid1Axes[3] =
{
mul(ellipsoid1Rotation, float3(1, 0, 0)).xyz,
mul(ellipsoid1Rotation, float3(0, 1, 0)).xyz,
mul(ellipsoid1Rotation, float3(0, 0, 1)).xyz,
};
float3 ellipsoid2Axes[3] =
{
mul(ellipsoid2Rotation, float3(1, 0, 0)).xyz,
mul(ellipsoid2Rotation, float3(0, 1, 0)).xyz,
mul(ellipsoid2Rotation, float3(0, 0, 1)).xyz,
};
float3 axes[15];
int axisIndex = 0;
// Ellipsoid 1 axes
for (int i = 0; i < 3; i++) {
axes[axisIndex++] = ellipsoid1Axes[i];
}
// Ellipsoid 2 axes
for (int i = 0; i < 3; i++) {
axes[axisIndex++] = ellipsoid2Axes[i];
}
// Cross product axes
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
axes[axisIndex++] = cross(ellipsoid1Axes[i], ellipsoid2Axes[j]);
}
}
float minOverlap = 1e20;
for (int i = 0; i < 15; i++)
{
float3 axis = normalize(axes[i]);
// Handle zero-length axis from cross product (parallel axes)
if (lengthSquared(axis) < 1e-6)
continue;
float ellipsoid1Min, ellipsoid1Max, ellipsoid2Min, ellipsoid2Max;
projectEllipsoid(axis, ellipsoid1Pos, ellipsoid1Rotation, ellipsoid1Extents, ellipsoid1Min, ellipsoid1Max);
projectEllipsoid(axis, ellipsoid2Pos, ellipsoid2Rotation, ellipsoid2Extents, ellipsoid2Min, ellipsoid2Max);
if (ellipsoid1Max < ellipsoid2Min || ellipsoid2Max < ellipsoid1Min)
{
result.collided = false;
return result; // Separating axis found.
}
float overlap = min(ellipsoid1Max, ellipsoid2Max) - max(ellipsoid1Min, ellipsoid2Min);
if (overlap < minOverlap)
{
minOverlap = overlap;
result.normal = dot(ellipsoid2Pos - ellipsoid1Pos, axis) > 0 ? axis : -axis;
result.depth = overlap;
}
}
result.normal = normalize(result.normal);
if (primaryFirst) { //Invert normal if required
result.normal = -result.normal;
}
result.collided = true; // No separating axis found.
return result;
}Box vs Ellipsoid Collision Detection
Applying Our Collisions
Now we have our collision data, what do we do with it? Well for now, lets just
CollisionResult result = boxBoxCollide(...); // Or any other collision function
if (result.collided)
{
// Calculate mass-weighted displacement
float totalInverseMass = (1.0f / mass1) + (1.0f / mass2);
// If one object is static (infinite mass), set its inverse mass to 0
if (isObject1Static) totalInverseMass -= (1.0f/mass1); //handle static objects.
if (isObject2Static) totalInverseMass -= (1.0f/mass2);
float3 displacement1 = -result.normal * (result.depth * (1.0f / mass1) / totalInverseMass);
float3 displacement2 = result.normal * (result.depth * (1.0f / mass2) / totalInverseMass);
// Apply displacements.
Positions[index1] += displacement1; // Assuming you have a Positions buffer
Positions[index2] += displacement2;
}We have also taken this opportunity of having collision normals to adjust the velocity with proper coefficients of friction and restitution (the elements of velocity aligned, or out of line with the collision normal). Fundamentally as we include our considerations of mass, we are ensure conservation of momentum when the collisions occur.
// --- Impulse Calculation (with Restitution and Friction) ---
float3 relativeVelocity = Velocities[index1] - Velocities[index2];
// --- Restitution ---
float restitution = 0.8f; // Coefficient of restitution (0.0 - 1.0)
float impulseMagnitude_n = dot(-(1.0f + restitution) * relativeVelocity, result.normal) / totalInverseMass;
float3 impulse_n = result.normal * impulseMagnitude_n;
// --- Friction (Simplified) ---
float friction = 0.5f; // Coefficient of friction (0.0 - 1.0)
// Calculate the tangential component of the relative velocity.
float3 tangent = relativeVelocity - dot(relativeVelocity, result.normal) * result.normal;
if(lengthSquared(tangent) > 0.0001) {// Avoid division by zero and normalize only if needed.
tangent = normalize(tangent);
}
// Calculate the magnitude of the friction impulse. This uses a simplified
// model of Coulomb friction: |friction impulse| <= mu * |normal impulse|
float impulseMagnitude_t = dot(-relativeVelocity, tangent) / totalInverseMass;
float3 impulse_t;
//Clamp the magnitude to be within the friction limit:
if(abs(impulseMagnitude_t) < friction * impulseMagnitude_n) {
impulse_t = tangent * impulseMagnitude_t;
} else {
impulse_t = tangent * -friction * impulseMagnitude_n; //dynamic friction
}
// --- Apply Impulses ---
//Only apply impulses if the object is not static
if(!isObject1Static) {
Velocities[index1] += (impulse_n + impulse_t) / Masses[index1];
}
if(!isObject2Static) {
Velocities[index2] -= (impulse_n + impulse_t) / Masses[index2];
}So, we’ve got the rigid body collisions defined, we’ve got the collision handing setup, let’s give it a whirl with a random selection of objects!
Ok, that’s what happens if your wall colliders are not properly setup, everything just goes flying off in it’s own direction. Actually I think it will be better to introduce perfectly elastic edges, instead of using colliders themselves. We can always add static colliders within the simulation box. Here’s a simple approach so each object can check for edge collisions after moving
float collisionDamping = 1;
float3 boundsSize = float3(GridExtents * 2.0, GridExtents * 2.0, GridExtents * 2.0);
float3 halfSize = boundsSize * 0.5;
float3 edgeDst = halfSize - abs(combinedObBuffer[iz].positionsBuffer); // (abs(pos) - float3(0.0, mapMinY, 0.0));
//Rebound by the amount of velocity not used already to get to edge;
//Reverse velocity and give the option to reduce;
if (edgeDst.x <= 0) {
combinedObBuffer[iz].positionsBuffer.x = (halfSize.x - (abs(combinedObBuffer[iz].velocitiesBuffer.x * deltaTime) - edgeDst.x)) * sign(combinedObBuffer[iz].positionsBuffer.x);
combinedObBuffer[iz].velocitiesBuffer.x *= -1 * collisionDamping;
}
if (edgeDst.y <= 0) {
combinedObBuffer[iz].positionsBuffer.y = (halfSize.y - (abs(combinedObBuffer[iz].velocitiesBuffer.y * deltaTime) - edgeDst.y)) * sign(combinedObBuffer[iz].positionsBuffer.y); //Rebound by the amount of velocity not used already to get to edge;
combinedObBuffer[iz].velocitiesBuffer.y *= -1 * collisionDamping; //Reverse and reduce;
}
if (edgeDst.z <= 0) {
combinedObBuffer[iz].positionsBuffer.z = (halfSize.z - (abs(combinedObBuffer[iz].velocitiesBuffer.z * deltaTime) - edgeDst.z)) * sign(combinedObBuffer[iz].positionsBuffer.z); //Rebound by the amount of velocity not used already to get to edge;
combinedObBuffer[iz].velocitiesBuffer.z *= -1 * collisionDamping; //Reverse and reduce;
}We’ve also added in a simulator grid outline so it’s a bit more obvious where the boundaries are, and also moved to lit shaders given we are trying to watch objects in 3D. Overall we can see the collisions detection seems to be working broadly well, but there seems to be an issue with objects getting conjoined or having strange rebound effects (likely due to the normals being the wrong way around).
/
